Why the Loss Surface of Deep Networks is broken
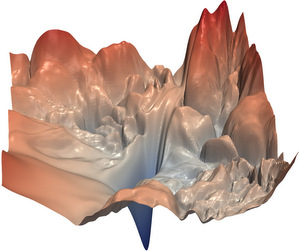
Studying loss surfaces is just a visual way of studying the optimization process of a neural network. My journey through the world of loss surfaces began when I first saw the following two images in a paper by Li et al.
| ResNet56 NoShort (source) | ResNet56 Short (source) |
|---|---|
 |
 |
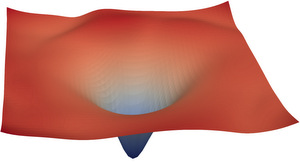The simplicity of the visualization just stuck me: the network corresponding to the loss surface on the left is obviously hard to train, since the surface is so rough that gradient descent has a hard time finding a good minimum. So we just have to find a network that makes the loss surface as smooth as a baby’s bottom and we solved deep learning, riight? That was about my naive thought process 5 years ago and I made this blog to share what I found out in the meantime.
Why is the loss surface so rough anyway?
Before going back to neural networks, let’s make a small excursion into electrical engeneering and talk about a phenomenon that most of you probably have experienced: shitty car speakers and the “bwt bwt bwt” sound they make instead of a bass.
This happens because you are cheap and your amplifier sucks the amplifier is asked make a sine wave with bigger amplitude than it can produce. The wave is then simply cut off at a certain amplitude, resulting in a kind of square wave (at least it sounds like hardstyle, right?). In electrical engeneering this is called a ringing artifact.
 |
 |
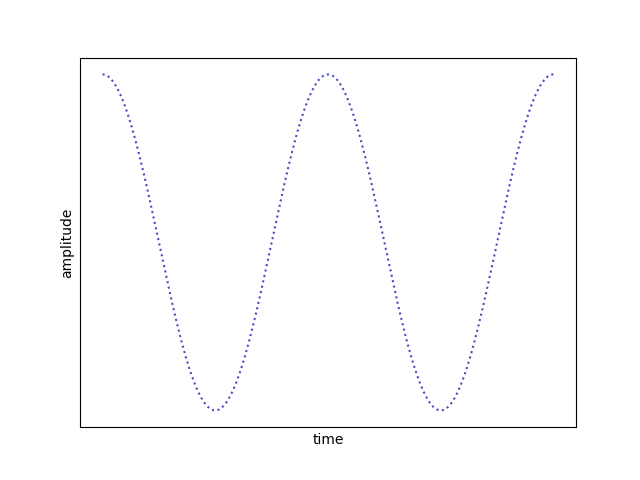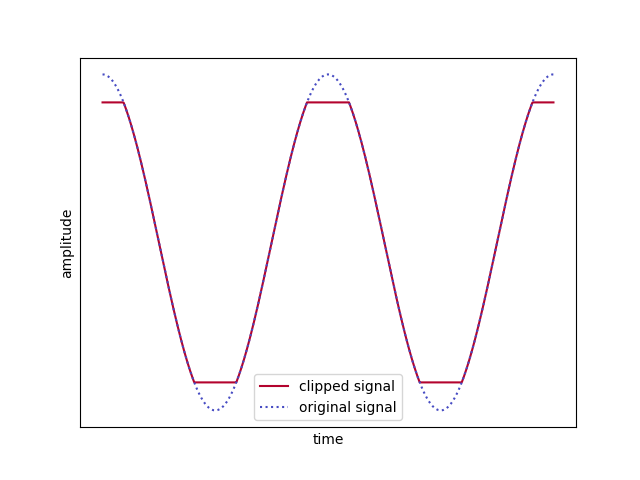This exact same principle also applies to neural networks since ReLU activation functions do more or less the same thing than the dysfunctional amplifier: clipping off all values below a threshold. For simplicity, let’s consider a 1-D loss path where we apply the ReLU activation function. When looking at the frequency spectrum (by using FFT) of a ReLU’d random path, we can clearly see the high frequent harmonics in the spectrum corresponding to the cutoff wave.
 |
 |
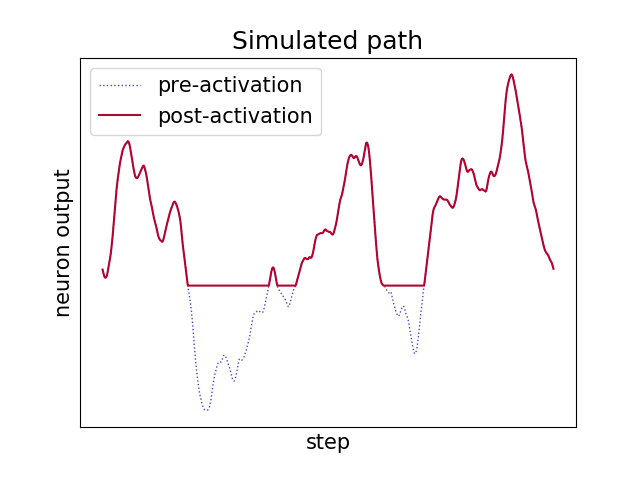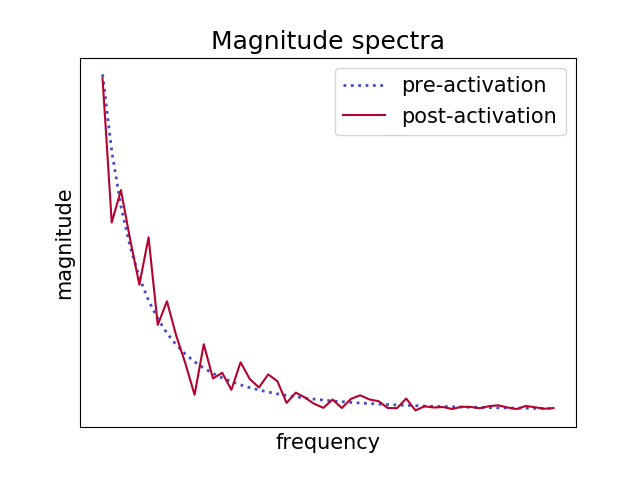Layer by layer, the surface is shifted and scaled, cutoff again, rinse and repeat. This is how the loss surface of a “NoShort” network like above becomes so rough and hard to optimize.
Measuring the Spectrum
Being scientists, we obviously had to verify wether our hypothesis holds true in real neural networks. By sampling the loss surface at each layer and computing its FFT, we can indeed see that the loss surface does get rougher with each additional layer.
Measured spectra of the loss surface at each layer of networks with different nonlinearities. Red lines correspond to the higher layers.
Interstingly enough, the amount of distortion depends on the nonlinearity used. Using a smooth(er) nonlinearity such as softplus does result in less distortion overall in the higher layers.
This is the first post in a series about loss surfaces. For a more formal writeup, check out our paper Ringing ReLUs