How ResNets fix the Loss Surface

In the last post of this series, we came to understand that harmonic distortions created by repeatedly applying ReLU layers are responsible for the rough loss landscape of deep neural networks. This created a dilemma for researchers: since the recent ascent of deep learning with the phenomenal success of AlexNet in deep learning, stacking layers and creating deeper networks was thought to be the root of their success. But at the same time very deep networks have a rough loss landscape because of harmonic distortions and are very hard to train without additional tricks.

One key event in overcoming these difficulties was the discovery of residual connections by Kaiming He et al. from Microsoft Research in 2015.

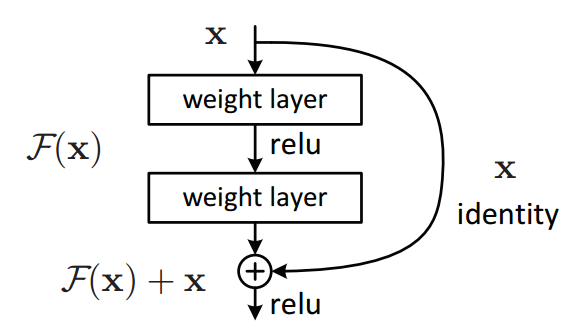
A residual block (source)

The idea boils down to adding “skip-connections” every two layers that basically add the untouched input of a residual block to its output. As we can see, this magically fixes the loss surface at merely the cost of an additional addition. But how does this black magic work?

ResNet56 NoShort (source)	ResNet56 Short (source)

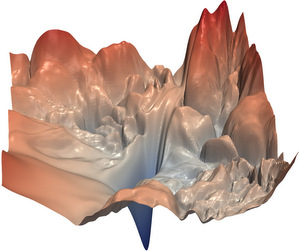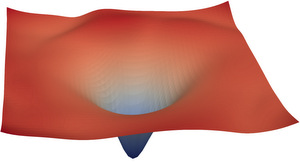We discovered two distinct mechanisms in a ResNet that “fix” the loss surface.

Exponential Downweighting (ED)

The first mechanism that allows ResNets to smoothen the loss surface is quite simple to understand. If every additional ReLU layer adds more high frequencies, higher layers in the network should contain more high frequencies than the lower layers. Consequently, by mixing the signal of a higher layer with a lower one, the resulting signal contains lesss high frquencies than the higher layer alone. This is exactly what a ResBlock is doing: mixing the signal of a higher layer with a lower one.

Simulated Path	Magnitude Spectrum

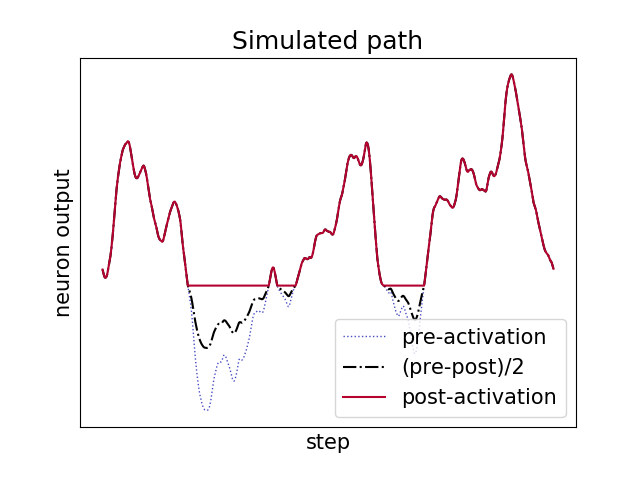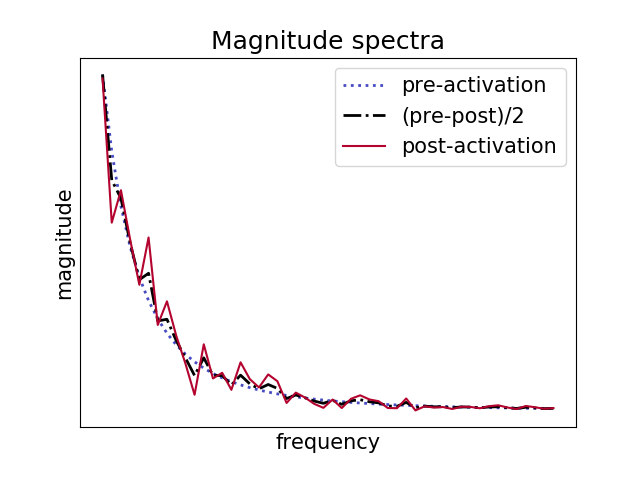To illustrate this effect, we simulated a random Fractional Brownian motion (FBM) path, applied the ReLU activation function to it and then averaged the result with the original path. As we can see above, the result is rougher than the initial path but not as rough as the non-averaged path.

Frequency Dependend Signal Averaging (FDSA)

The second effect that allows ResNets to dampen high frequencies in the loss surface is similar to something that modern cellphone cameras do to reduce noise in pictures: signal averaging. Asssume we have an image $i\in\mathbb{R}^{n\times m}$ that is composed of a signal $s$ and noise $n$: $i=s+n,$

where the noise is Gaussian: $n\sim\mathcal{N}(0,Var(n))$. Let’s say that we have 10 different images of the same motive $i_1, \dots, i_{10}$ with the same signal $s$ but independent noise components $n_1, \dots, n_{10}$. If we simply average our 10 images, we obtain the following:

$i_{avg} = \frac{1}{10} \sum_{i=1}^{10} i_i = \frac{1}{10} \sum_{i=1}^{10} s + n_i = s + \frac{1}{10} \sum_{i=1}^{10} n_i.$

Computing the variance of the noise of $i_{avg}$, we obtain:

$Var(n_{i_avg}) = Var(\frac{1}{10} \sum_{i=1}^{10} n_i) = \frac{1}{10^2} \sum_{i=1}^{10} Var(n_i) = \frac{1}{10} Var(n_i) .$

The noise is reduced by a factor 10! Here a visual example of the Duomo in Florence: we created 10 noisy copies (middle) of the original photo (left) and averaged them (right). We can see that the averaged image contains much less noise than the noisy images.

Original Image	Image with Noise	Averaged Image

An interesting extension of this theory is that the noise components in two images noisy $i_1$ and $i_2$ don’t have to be completely uncorrelated for this to work. Assuming that $n_1$ and $n_2$ are not independent, we obtain:

$Var(n_1 + n_2) = Var(n_1) + Var(n_2) + Cov(n_1,n_2)$

This means that as long as the signal is more correlated than the noise, we still get a relative gain in signal strength!

We conjectured that something similar is happening inside a residual block: the high frequencies that are created by the two additional ReLU layers in the network depend on the weights of the weight layers in ResBlock. Since the residual branch is equivalent to the input of the block that has not yet seen any of the weights inside of the block, it would be very surprising if the high frequencies in both branches would be strongly correlated. We confirmed this theory by measuring the correlation of the loss surface of the main branch and the residual branch inside a ResNet at initialization and obtained the results below.

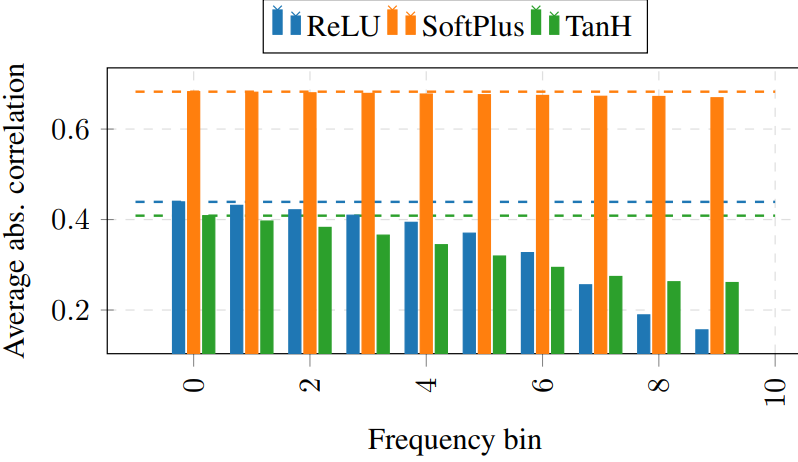
Correlation of the loss surfaces of the main and residual branch in different frequency bins in a ResNet56

We see that indeed for all three nonlinearities used the correlation is decaying for higher frequencies and therefore leads to a relative dampening in high frequencies.

Why these effects can be cumulative

Fundamentally, ED and FDSA can happen at the same time and result in culumaltive dampening. This can be understood quicky observing the following illustrations.

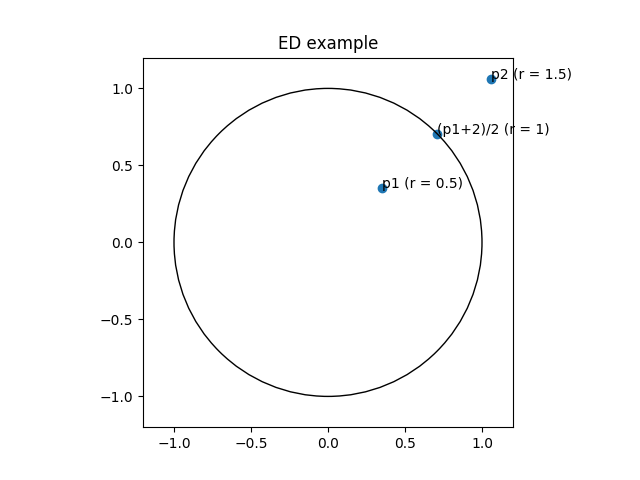
ED can be understood as averaging two complex numbers with a different radii. The resulting point’s radius then is inbetween the two initial radii and thus smaller than the bigger one.

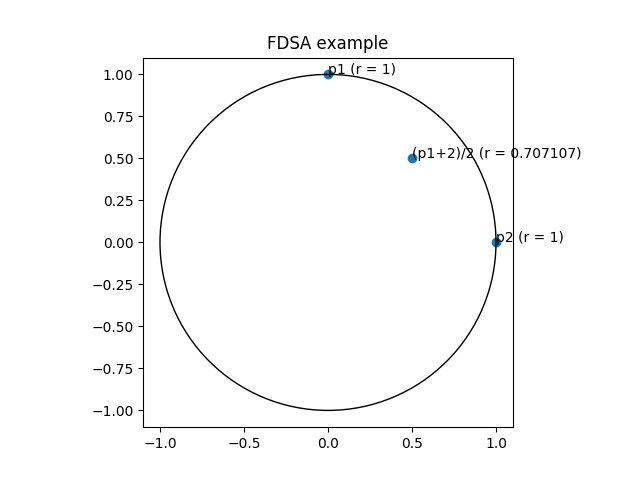
FDSA can be understood as averaging two complex numbers in polar coordinates with unit radius. If the points have a different angle, averaging the points results in a point with a lower radius.

In the above example both effects act cumulatively: ED only would result in a point with radius $\frac{0.5 + 1.5}{2}=1$, but in the resulting point’s radius is well below $1$!

Multipath networks

In order to validate the presence of FDSA without ED in real neural networks, we took a closer look at multipath architectures. Multipath architectures take the layer input and process it on multiple, independent branches. Using the same argument as above, the high frequencies created in the loss surface of the different branches should not be strongly correlated between each other, since they depend on the weights in the respective branches which are not shared between branches!

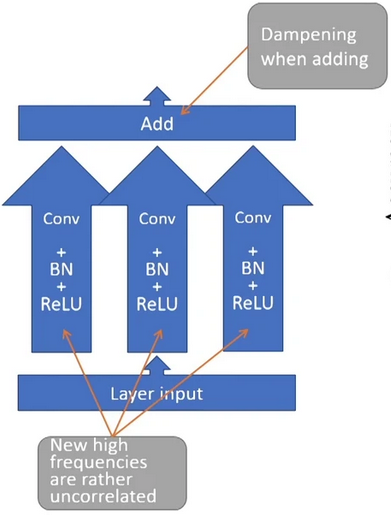
Multipath networks create rather uncorrelated high frequencies.

Our experimental setup is the following: we modified our basic ResNet56 “NoShort” to have $a$ independent computation paths that get averaged at the end of each ResBlock instead of one. We purposefully use a network without residual connections to exclude an additional ED effect. We then measured and compared the spectrum at initialization and training accuracy of networks for different values of $a$. Since the multipath networks contain more parameters than the regular network, the comparison is not totally fair. We therefore added a wide single-path network that has as many neurons as the $a=3$ multipath network for reference.

Performance and spectrum at initialization of multipath networks.

As we can see on the right side of the figure, multiple computation paths indeed dampen the spectrum due to the FDSA effect. The training performance of the networks without skip-connections is indeed higher for the 3-path network than for the 1-path network, even comparing to a 1-path network with as many neurons as the 3-path network. The multipath networks still cannot reach the performance of a network with skip-connections, even for higher values of $a$: this is consistent with our theory that ResNets also additionaly leverage the ED effect, which is stronger than FDSA alone.

This is the first post in a series about loss surfaces. For a more formal writeup, check out our paper Ringing ReLUs